В данной статье описана реализация метода градиентного спуска в программе MatLab.
Ключевые слова: поиск минимума, поиск экстремума, оптимизация, метод градиентного спуска, метод наискорейшего спуска.
Введение.
Машинное обучение сейчас занимает чуть ли не первое место среди наиболее быстро развивающихся направлений науки и является очень перспективным направлением для различных разработок. В современном машинном обучении применяется множество математических методов и алгоритмов оптимизации. Один из них — метод градиентного спуска.
Градиентный спуск — это алгоритм оптимизации, используемый для минимизации ошибок в модели машинного обучения. Особенно большой интерес к градиентным методам в последние годы связан с тем, что градиентные спуски и их рандомизированные варианты лежат в основе почти всех современных алгоритмов обучения, разрабатываемых в анализе данных [1]. Теперь подробнее рассмотрим суть метода.
Идея метода.
Задача — поиск минимума некоторой функции с начальным приближением (некоторой точкой, в окрестности которой возможно наблюдается экстремум). Главное условие работы метода — возможность вычисления градиента этой функции. Суть метода заключается в том, чтобы “двигаться” (осуществляя тем самым оптимизацию) в направлении антиградиента (то есть направлении наискорейшего спуска — из-за этого метод иногда называют методом наискорейшего спуска); но для реализации этой идеи нам потребуется умножать антиградиент функции на некоторое число, которое может быть как постоянным, так и меняться (в нашем случае будет использоваться постоянное), чтобы не “перепрыгнуть” экстремум при первой итерации и не потерять точность при последующих (при постоянной
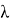
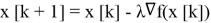
Алгоритм.
Имея формулу, предложенную выше несложно описать алгоритм, ищущий минимум функции данным методом. Таким образом нужно:
-
Циклически выполнять описанное в формуле действие:
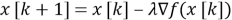
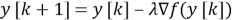
-
При срабатывании одного из критериев останова (которых довольно много) останавливать процесс. Причем критерий останова работает на основе вводимого параметра
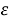
- Последняя полученная точка будет найденным минимумом.
Реализация.
Описанный алгоритм был реализован в виде отдельной функции, экспериментально выбрав критерий останова, который давал наибольшую точность (подробности реализации конкретного критерия можно увидеть в коде MatLab, представленном в листинге 3);
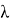
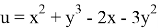
|
«Стандартный» метод: Точка (1.0000, 2.0000) является минимумом. Значение функции в данной точке: -5.0000 Метод градиентного спуска: Точка (1.0158, 2.0000) является экстремумом. Количество итераций, потребовавшихся для поиска: 275 |
Таким образом мы видим, что метод градиентного спуска работает с некоторой точностью, и она ограничена, в данном случае, тем, что по y функция “пришла” к точке, в которой наблюдается экстремум, быстрее (причем, как выяснилось, зависимость от
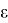
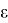
Графики:
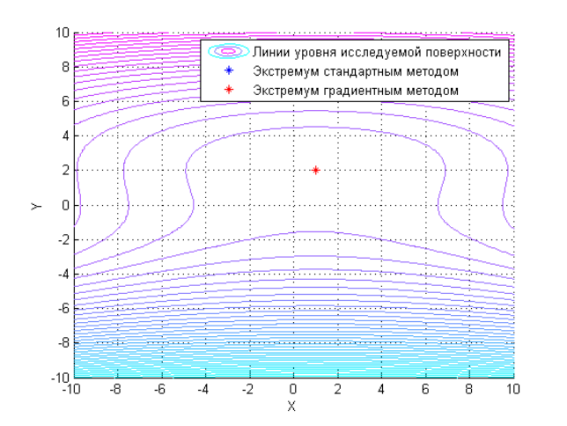
Рис. 1. Найденные экстремумы, двумерный вид
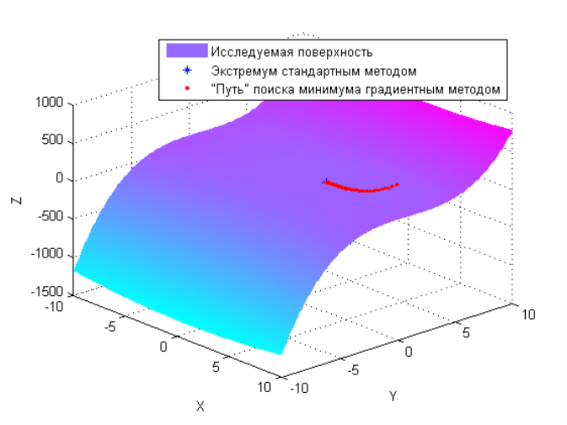
Рис. 2. “Путь” градиентного метода, трехмерный вид
Код основной программы:
|
clear clf clc close hold on grid on syms x y %Записываем функцию и ищем двумя методами f=x^2+y^3-2*x-3*y^2; %Поверхность [X Y]=meshgrid(-10:.1:10); Z=X.^2+Y.^3-2.*X-3.*Y.^2; surf (X,Y,Z); fprintf('"Стандартный" метод:\n'); [a,b]=ex(f); plot3(a,b,subs(f,{x,y},[a,b]),'*b'); fprintf('Метод градиентного спуска:\n'); [U,I,iter]=gradient_descent(5,5,f,0.001); fprintf('Точка (%.4f,%.4f) является экстремумом. Количество итераций, потребовавшихся для поиска: %d\n',double(U),double(I),double(iter)); colormap cool shading interp legend('Исследуемая поверхность','Экстремум стандартным методом','"Путь" поиска минимума градиентным методом'); %axis([-2 6 0 7]); xlabel('X'); ylabel('Y'); zlabel('Z'); figure; hold on grid on contour(X,Y,Z,50); plot(a,b,'*b'); plot(U,I,'*r'); colormap cool shading interp legend('Линии уровня исследуемой поверхности','Экстремум стандартным методом','Экстремум градиентным методом'); xlabel('X'); ylabel('Y'); |
Рис. 3. Листинг 1. Код программы
Код функции ex:
|
function[out1, out2]=ex(f) syms x y; dfx=diff(f,x); dfy=diff(f,y); d1=diff(dfx,x); d2=diff(dfx,y); d3=diff(dfy,y); [a,b]=solve(dfx,dfy); a=a(abs(imag(double(a)))<10^(-8)); b=b(abs(imag(double(a)))<10^(-8)); for i=1:length(a) A=subs(subs(d1,x,a(i)),y,b(i)); B=subs(subs(d2,x,a(i)),y,b(i)); C=subs(subs(d3,x,a(i)),y,b(i)); D=double(A*C-B^2); z=subs(subs(f,x,a(i)),y,b(i)); if D>0 if A>0 fprintf('Точка (%.4f,%.4f) является минимумом. Значение функции в данной точке: %.4f\n',double(a(i)),double(b(i)),double(z)); out1=a(i); out2=b(i); else fprintf('Точка (%.4f,%.4f) является максимумом. Значение функции в данной точке: %.4f\n',double(a(i)),double(b(i)),double(z)); out1=a(i); out2=b(i); end elseif D<0 %fprintf('Точка (%.2f,%.2f) не является экстремумом.\n',double(a(i)),double(b(i))); else fprintf('Точка (%.2f,%.2f) требует дополнительных исследований.\n',double(a(i)),double(b(i))); end end end |
Рис. 4. Листинг 2. Код функции ex
Код функции gradient_descent:
|
function[out1,out2,out3]=gradient_descent(g,h,f,eps) hold on grid on k=1; lm=0.01; %delta=0.9; X(1)=g; Y(1)=h; syms x y diff(f,x); diff(f,y); while (k<1000) X(k+1)=X(k)-lm*(subs(diff(f,x),x,X(k))); Y(k+1)=Y(k)-lm*(subs(diff(f,y),y,Y(k))); %Лучшая проверка: CND1=(((subs(diff(f,x),x,X(k)))^2 + (subs(diff(f,y),y,Y(k)))^2) <= eps); %Хорошая проверка %CND2=((abs(subs(subs(f,x,X(k+1)),y,Y(k+1))-subs(subs(f,x,X(k)),y,Y(k)))) <=eps); if CND1 out1=X(k+1); out2=Y(k+1); break End k=k+1; plot3(X(k),Y(k),subs(f,{x,y},[X(k),Y(k)]),'.r') end out1=X(k); out2=Y(k); out3=k; if k==1000 disp('Перебор...') end end |
Рис. 5. Листинг 3. Код функции gradient_descent
Литература:
- Градиентный спуск — Википедия // ВикипедиЯ URL: https://ru.wikipedia.org/wiki/Градиентный_спуск (дата обращения: 25.01.24).
- Горлач Б. А., Шахов, В. Г. Математическое моделирование. Построение моделей и численная реализация: Учебное пособие. — СПб.: Издательство «Лань», 2016. — 292 c. — (Учебники для вузов. Специальная литература) https://e.lanbook.com/reader/book/169100/#99.
- Горлач Б. А. Математический анализ: Учебное пособие. — СПб.: Издательство «Лань», 2013. — 608 с.: ил. — (Учебники для вузов. Специальная литература) https://e.lanbook.com/reader/book/4863/#316.
- Вычислительные методы линейной алгебры [Текст] / Д. К. Фаддеев, В. Н. Фаддеева. — 3-е изд., стер. — Санкт-Петербург: Лань, 2002. — 733 с.: ил., табл.; 20 см.; ISBN 5–8114–0317–8.

