В статье рассматривается разработка прикладного программного продукта для автоматизированного решения задач дискретной оптимизации. Представлены структура и архитектура веб-приложения, особенности реализации модулей задачи о назначениях, транспортной задачи и задачи поиска кратчайшего пути. Особое внимание уделено визуализации алгоритмов и хранению истории решений как элементам образовательной направленности системы.

Ключевые слова: дискретная оптимизация, веб-приложение, визуализация алгоритмов, Венгерский метод, алгоритм Дейкстры, метод потенциалов, транспортная задача, поиск кратчайшего пути, задача о назначениях, Flask, Cytoscape.js, Python, SQLite.

The article discusses the development of an application software product for solving discrete optimization problems. The structure and architecture of the web application are presented, as well as implementation features of modules for the assignment problem, transportation problem, and shortest path search. Particular attention is paid to the visualization of algorithms and storing the history of solutions as tools for educational use.

Keywords: discrete optimization, web application, algorithm visualization, Hungarian method, Dijkstra's algorithm, potential method, transportation problem, shortest path search, assignment problem, Flask, Cytoscape.js, Python, SQLite.

Введение

Дискретная оптимизация — это область математического программирования, нацеленная на поиск экстремумов целевых функций при условии, что переменные принимают дискретные значения. К числу типичных задач относятся задача о назначениях, транспортная задача, задача коммивояжёра и поиск кратчайшего пути. Они имеют широкое применение в логистике, производственном планировании, информационных системах и образовании [1].

Разработка специализированных программных средств для решения таких задач позволяет автоматизировать вычисления, обеспечить удобство использования и создать платформу для обучения алгоритмическим методам. Особенно актуальны решения с открытой архитектурой и визуализацией.

Настоящая статья посвящена описанию веб-приложения, реализующего решение трёх базовых задач дискретной оптимизации: задачи о назначениях (с использованием Венгерского метода), транспортной задачи (метод потенциалов), задачи поиска кратчайшего пути (алгоритм Дейкстры). В работе рассмотрены архитектура системы, интерфейс, алгоритмы, используемые библиотеки, а также преимущества реализованного подхода.

Основная часть 1. Архитектура и компоненты веб-приложения

Разрабатываемая система построена по модульной архитектуре с использованием подхода Model–View–Controller (MVC), что обеспечивает расширяемость, читаемость и тестируемость кода [2]. Архитектура включает три уровня:

Model — отвечает за хранение и обработку данных, реализуется средствами СУБД SQLite;

View — визуальное отображение пользовательского интерфейса, построенное с использованием HTML, Tailwind CSS и библиотеки Cytoscape.js;

Controller — бизнес-логика и маршрутизация, реализуемые на сервере с использованием микрофреймворка Flask на языке Python.

Вся логика приложения разбита на независимые модули:

— assignment — модуль решения задачи о назначениях;

— transport — модуль транспортной задачи;

— dijkstra — модуль поиска кратчайшего пути;

— history — хранение и отображение истории решений;

— core — навигация и базовые маршруты.

Каждый модуль включает обработку пользовательского ввода, выполнение алгоритма и визуализацию результата.

2. Выбор технологий и библиотек

Выбор технологий был обусловлен следующими требованиями:

— кроссплатформенность;

— простота развертывания;

— высокая скорость разработки;

— наличие открытых библиотек.

Серверная часть:

Python — основной язык реализации, обладающий богатой системой библиотек для математических расчётов [3];

Flask — веб-фреймворк, позволяющий гибко управлять логикой приложения [4];

SQLite — встроенная база данных, не требующая отдельного сервера.

Клиентская часть:

HTML5 + Tailwind CSS — быстрая стилизация интерфейса через утилитарные классы [5];

JavaScript — интерактивность, динамическое управление DOM;

Cytoscape.js — визуализация графов в браузере, используется в модуле кратчайшего пути для ввода графа [6].

Алгоритмы:

Венгерский метод + scipy.optimize.linear_sum_assignment — решение задачи о назначениях;

алгоритм Дейкстры — реализация с приоритетной очередью (heapq) для решения задачи поиска кратчайшего пути;

метод потенциалов — для решения транспортной задачи.

3. Реализация модулей

Поиск кратчайшего пути

Работа модуля поиска кратчайшего пути, представленная на рисунке 1, начинается с того, что пользователь вручную формирует граф на веб-интерфейсе с помощью библиотеки Cytoscape.js. Он добавляет вершины и рёбра, при необходимости задаёт веса, и указывает начальную и целевую вершины. После нажатия кнопки «Рассчитать» граф автоматически преобразуется в сериализованный JSON, в котором хранится информация о структуре и весах рёбер.

Этот JSON отправляется на серверное приложение, реализованное на Flask. На сервере данные обрабатываются: из них строится список смежности, пригодный для выполнения алгоритма Дейкстры. Алгоритм реализован вручную: используется приоритетная очередь, массивы расстояний и предков для трассировки кратчайших путей.

После завершения вычислений формируется результат: это кратчайшее расстояние от начальной до целевой вершины, а также сам путь, представленный в виде последовательности вершин. Результат возвращается обратно в браузер, где визуализируется: на исходном графе выделяется кратчайший путь (цветом и толщиной рёбер), а также отображается таблица со всеми расстояниями от начальной вершины до остальных.

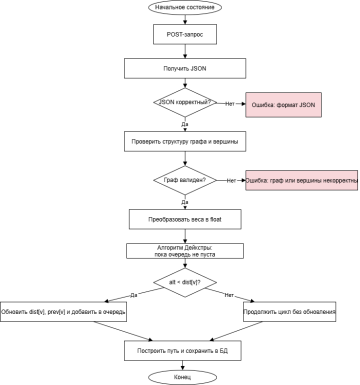
Рис. 1. Блок-схема модуля решения задачи поиска кратчайшего пути

Задача о назначениях

Модуль задачи о назначениях начинается с ручного ввода пользователем квадратной или прямоугольной матрицы стоимости, где строки представляют исполнителей, а столбцы — задачи. Пользователь может редактировать значения прямо в таблице на странице. После ввода и запуска алгоритма происходит передача матрицы на сервер.

На серверной части используется функция linear_sum_assignment из библиотеки scipy.optimize, реализующая Венгерский метод [7]. Однако, помимо получения конечного результата, в системе предусмотрен вывод пошаговых преобразований: изначально проводится вычитание минимальных значений по строкам, затем по столбцам. Построенная нулевая матрица используется для поиска допустимых назначений — с вычёркиванием строк и столбцов, покрытием минимальным числом линий и определением следующего шага.

Если оптимальное назначение ещё не найдено, то производится коррекция матрицы: от непокрытых элементов вычитается минимум, к элементам на пересечении — прибавляется. Процесс повторяется, пока не получится разбиение с нужным количеством назначений. Затем формируется результат: список пар «исполнитель–задача», итоговая стоимость и визуализация всех шагов на интерактивной матрице, где цветом выделяются нули, вычеркнутые элементы и финальные связи.

Рис. 2. Блок-схема модуля решения задачи о назначениях

Транспортная задача

Работа модуля транспортной задачи начинается с ввода пользователем таблицы затрат между поставщиками и потребителями, а также объёмов поставок и потребления. Если суммарные объёмы не равны, система автоматически балансирует задачу, добавляя фиктивного участника (поставщика или потребителя).

На следующем этапе строится начальный опорный план с помощью метода северо-западного угла: начинается заполнение ячеек таблицы с левого верхнего угла, с постепенным вычитанием объёмов. Полученная базисная структура сохраняется и подаётся на оптимизацию методом потенциалов.

Метод потенциалов предполагает расчёт потенциалов строк (u) и столбцов (v), на основе которых определяется оценка для каждой небазисной ячейки. Если хотя бы в одной ячейке оценка отрицательная, план не оптимален. В этом случае производится построение замкнутого цикла, пересчёт значений и обновление перевозок.

Когда все оценки неотрицательны, решение считается оптимальным. Программа формирует итоговую таблицу перевозок, в которой указаны объёмы перемещений по маршрутам и суммарная стоимость. Отдельно отображаются базисные клетки, потенциалы, оценки и шаги корректировки в табличном формате.

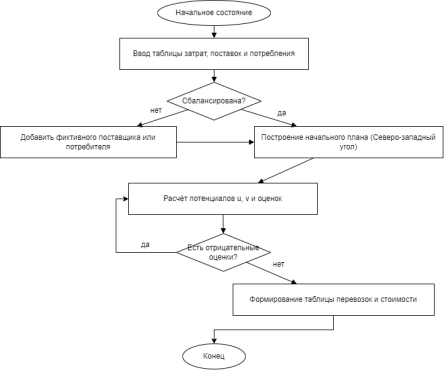
Рис. 3. Блок-схема модуля решения транспортной задачи

4. Визуализация и образовательная направленность

Одной из ключевых особенностей разработанного веб-приложения является визуализированная реализация вычислительных алгоритмов. Это отличает продукт от большинства существующих решений, в которых результаты представляются в виде финальных чисел, без раскрытия логики вычислений.

Визуализация служит двум основным целям:

Повышение наглядности и доверия к результатам — пользователю демонстрируется весь ход алгоритма: от вычитания минимумов в матрице до финального сопоставления исполнителей и задач.

Образовательная ценность — пошаговое выполнение алгоритмов делает систему подходящей для использования в учебных курсах по дискретной математике, исследованию операций, теории графов и оптимизации.

Примеры визуализированных элементов:

Подсветка выбранных нулей и вычеркнутых элементов в матрице (задача о назначениях);

Таблицы потенциалов, базисных ячеек и оценок (транспортная задача);

Интерактивный граф с выделением кратчайшего пути, трассировочной таблицей и шагами пересчёта (поиск пути).

Интерфейс поддерживает работу в браузерах Google Chrome, Mozilla Firefox и Opera. Отдельный модуль истории позволяет сохранить и повторно проанализировать каждый расчёт, что важно при обучении и повторном тестировании.

Заключение

Разработанное веб-приложение демонстрирует возможности интеграции классических методов дискретной оптимизации с современными веб-технологиями. Продукт реализует три ключевые задачи — о назначениях, транспортную и поиск кратчайшего пути — с упором на:

— модульность архитектуры (MVC, Flask Blueprint),

— наглядность интерфейса (Tailwind CSS, Cytoscape.js),

— образовательную ценность (пошаговые алгоритмы, история решений).

Система является кроссплатформенной, автономной и легко масштабируемой: в будущем возможно добавление новых типов задач, расширение аналитики, интеграция с LMS и другими платформами.

Проект может быть использован в учебных целях как интерактивное средство изучения методов оптимизации.

Литература:

1. Хилльер Ф., Либерман Г. Введение в исследование операций. — М.: Вильямс, 2005. — 1088 с.
2. Гамма Э. и др. Приёмы объектно-ориентированного проектирования. — СПб.: Питер, 2018. — 368 с.
3. Лутц М. Изучаем Python. 5-е изд. — СПб.: Питер, 2016. — 1216 с.
4. Grinberg M. Flask Web Development. — O'Reilly Media, 2018.
5. Tailwind Labs. Tailwind CSS Documentation. https://tailwindcss.com/docs
6. Cytoscape.js. https://js.cytoscape.org/
7. SciPy. Optimize: linear_sum_assignment. https://docs.scipy.org/
8. Дьяконов В. П. Методы и средства дискретной оптимизации. — М.: Радио и связь, 2002.
9. Алексеев П. О. Universum: технические науки. — 2025. — № 4(133). — С. 26–33.