Рассматриваются примеры трисекции угла. Объясняется как решать задачи о делении угла на равные части с помощью циркуля и линейки.

Ключевые слова: угол, циркуль, линейка, трисекция угла.

Задача о трисекции угла наряду с еще двумя известными задачами на построение: удвоением куба и квадратурой угла, пришла ещё с Древней Греции. В течении нескольких тысячелетий эти три задачи привлекали внимание многих математиков, уже тогда они понимали, что решить их используя исключительно циркуль и линейку невозможно, и доказали это значительно позднее. По сравнению с двумя другими задачами, задача о трисекции угла является менее известной. Есть несколько моментов, в которых задача разделения угла на три части отличается от двух других классических греческих задач. Во-первых, она не имеет реальной истории, относящейся к тому, почему эту задачу впервые начали изучать. Во-вторых, это задача совершенно другого типа. Никто не может построить квадрат, равный по площади никакому кругу, не может построить ребро куба, объем которого в два раза больше объема никакого данного куба.

Происхождение задачи о трисекции угла также связано с практической деятельностью. В частности, уметь делить окружность на равные части нужно было при изготовлении колеса со спицами, деление угла или дуги окружности на несколько равных частей необходимо было и в архитектуре, в создании орнаментов, в строительной технике и в астрономии.

С помощью циркуля и линейки для n=6 и 8 правильные n-угольники построить можно, а для n =7 и 9 нельзя. Построение правильного семиугольника — интересная задача: ее можно решить с помощью способа «вставок». Построение правильного семиугольника предложил Архимед. А вот попытки построить правильный девятиугольник как раз и должны были привести к задаче трисекции угла, потому что для построения правильного девятиугольника нужно было построить угол

,т. е. разделить угол 120° на три равные части.

Теперь же рассмотрим методы решения данной задачи.

Методы решения

Прежде чем рассмотреть все методы решения, выясним как возникла эта проблема естественным образом. Возможно, задача впервые появилась, при изучении того, как делить угол пополам с помощью циркуля и линейки.

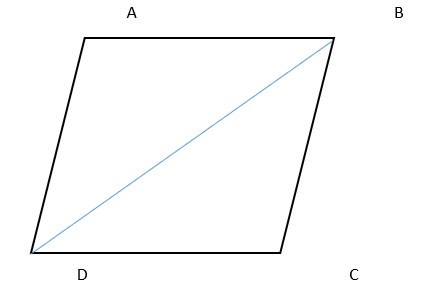
Для этого достаточно построить ромб, и провести диагональ , которая поделит пополам .

Метод первый (метод, который был известен Гиппократу)

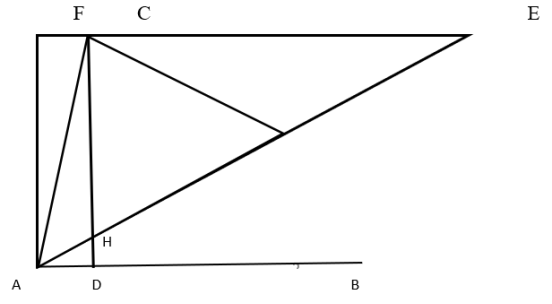
Этот способ состоит в следующем. Для данного угла проведем прямую перпендикулярно прямой , пересекающую ее в точке . Построим прямоугольник . Продлим до точки , и пусть пересекает в точке . Если точка выбрана так, что , то угол составляет угла .

Чтобы убедиться в этом, обозначим через середину , так что . Так как угол прямой, то . Кроме того, . Поскольку , . Но , что, собственно, нам и требовалось.

Метод второй (решение при помощи спирали Архимеда)

Архимедова спираль — спираль, плоская кривая, траектория точки L которая равномерно движется вдоль луча OA с началом в O, в то время как сам луч OA равномерно вращается вокруг O.

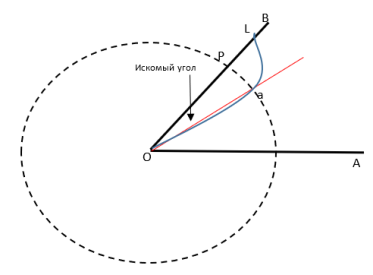
Эта кривая получается следующим образом. Пусть луч ОА равномерно вращается вокруг точки О, а точка L равномерно движется по этому лучу, причем в начальном положении она находится в точке О. Тогда точка L движется по спирали Архимеда. Пусть угол АОВ нужно разделить в заданном отношении. Рассмотрим часть спирали Архимеда, полученную при вращении луча от начального положения ОА до положения ОВ. Пусть Р—точка, которая делит OL в отношении 1:2, где L — точка пересечения луча ОВ и спирали, Q — точка пересечения спирали и окружности радиуса ОР с центром О. Из определения спирали следует, что LOQ: QOA = LP:QO = LP: PO= 1:2, т. е. OQ —искомый луч и LOQ=BOA/3.

Метод третий (решение сиспользованием гиперболы)

В своей работе под названием “Математическое собрание” Папп приводит два решения нашей проблемы, и обе они включают в себя рисование гиперболы.

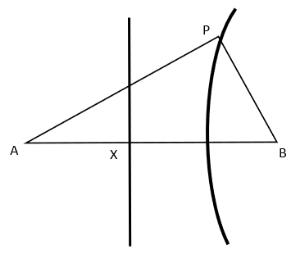
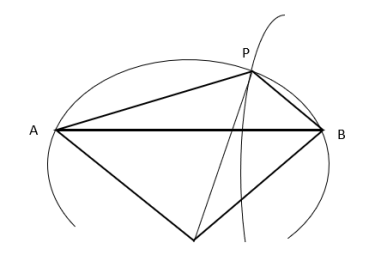
Первый показывает, что если прямая фиксирована, то геометрическое место точек таких, что является гиперболой. Гипербола имеет эксцентриситет 2, фокус и директрису, которая является серединным перпендикуляром . Гипербола изображена в левой части рисунка. Справа на двух рисунках показано, как эта гипербола может быть использована для деления на три равные части угла . Проведем окружность с центром в точке через точки и . Затем построим гиперболу с эксцентриситетом 2, фокусом и директрисой — серединным перпендикуляром к . Пусть она пересечет окружность в точке . Тогда отделяет треть угла .

Чтобы убедиться в этом, заметим, что из свойств гиперболы, описанных выше, . Но , и (центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу). Поэтому , что и требовалось.

Гаусс заявил, что проблемы удвоения куба и трисекции угла не могут быть решены с помощью циркуля и линейки, но он не привел никаких доказательств этому. В своей работе 1837 года Ванцель первым доказал эти результаты. Позднее Чарльз Штурм улучшил эти доказательства, но он не опубликовал их.

Заключение

После написания этой статьи, я узнала много нового и интересного о знаменитых классических задачах древности, познакомилась с историей возникновения данных задач, методами их решения.

неразрешимые задачи на построение сыграли особую роль в истории математики. В конце концов, было доказано, что эти задачи невозможно решить, пользуясь только циркулем и линейкой. Но уже сама постановка задачи — «доказать неразрешимость» — была смелым шагом вперёд.

Вместе с тем предлагалось множество решений при помощи нетрадиционных инструментов. Всё это привело к возникновению и развитию совершенно новых идей в геометрии и алгебре.

Закончив и проанализировав свою исследовательскую работу, я сделала следующие выводы:

– возникновение подобных задач обуславливалось их практической значимостью (в частности, построение правильных многоугольников);

– подобные задачи вызывают развитие новых методов и теорий;

– неразрешимые задачи привлекают больше внимания к наукам:

Изучив весь этот материал, я поняла, что все старания решить три знаменитые задачи при известных ограничивающих условиях (циркуль и линейка) привели только к доказательству, что подобное решение невозможно. Но, несмотря на это, интерес к этим классическим задачам не пропадает и сегодня. Многие современные математики пытаются их решить и по сей день.

Литература:

1. Прасолов В. В. Три классические задачи на построение: удвоение куба, трисекция угла, квадратура круга.— М.: Наука. Гл. ред. физ.-мат. лит., 1992. — 80 с. (Популярные лекции по математике; Вып. 62).
2. История математики с древнейших времён до начала ХIХ столетия. В трёх томах. Том I. Под редакцией А. П. Юшкевича.– М.: Наука. — 353 с.
3. В. Прасолов. Три классические задачи на построение. Москва «Наука», 1992.
4. П. Савин. Математика. Энциклопедия для детей. Москва «Аванта +», 1998.