При решении экспериментальных задач по физике часто возникает необходимость измерения физических величин, находящихся в функциональной зависимости. Как правило, после измерений информация о физическом явлении извлекается из графиков, построенных по данным, полученным экспериментальным путем, а зависимость между двумя физическими величинами — xи yпредставляется в виде таблицы 1.

Таблица 1

В связи с тем, что значения величин xи y измеряются с погрешностью, нанесенные на координатную плоскость точки будут разбросаны относительно предполагаемой кривой.

Если график y = f (x) строить, непосредственно соединяя экспериментально полученные точки, то он будет иметь вид ломаной. Однако в большинстве случаев функции, описывающие процессы в природе, являются гладкими. Значит, необходимо подобрать такую функцию y = f (x), которая наилучшим образом выражала бы экспериментальную зависимость y от x.

Наиболее простым видом функциональной зависимости является прямо пропорциональная зависимость между физическими величинами вида.

Необходимо отыскать такой коэффициент k, а значит, прямую, наилучшим образом согласованную с экспериментальными точками, нанесенными на плоскость (x, y), при котором общее отклонение

минимально (рисунок 1). Для этого необходимо решить уравнение:

или ,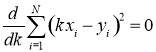

где xi, yi — измеренные значения величин; N — количество пар значений измеренных величин.

Естественно, что для отыскания экстремума дифференцирование ведется по параметру, от которого зависит, как пройдет график. Воспользовавшись правилами дифференцирования суммы и сложной функции, получим

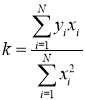
Полученное значение параметра k позволяет наиболее близко к экспериментальным точкам провести прямую, выходящую из начала координат.

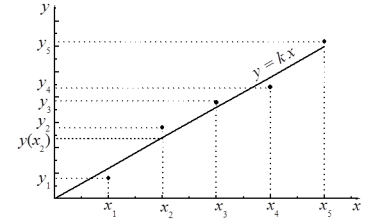
Рис. 1. Экспериментальные точки при измерении величин

Погрешность при определении параметра k:

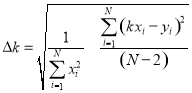
Экспериментальная задача. Измерить сопротивление проводника при помощи амперметра и вольтметра. Оценить погрешность измерений.

Для решения поставленной задачи необходимо собрать электрическую цепь, изображенную на рисунке 2.

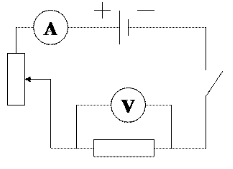
Рис. 2. Экспериментальная установка для измерения сопротивления проводника при помощи амперметра и вольтметра

Изменения силы тока и напряжения на резисторе, полученные в результате измерений приведены в таблице 2.

Таблица 2

Необходимо подобрать такую формулу U = f (I), чтобы она наиболее удачно отражала зависимость между силой тока I и напряжением U. Закон Ома устанавливает эту зависимость в виде U=RI. Это линейная зависимость. Определим величину сопротивления R.

Способ № 1.

1.                Определим значение сопротивления R каждого из N измерений:

.

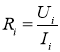2.                Определим среднее значение сопротивления по формуле:

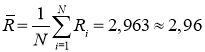(Ом).

Погрешность такого косвенного измерения сопротивления можно найти по правилам обработки результатов прямых измерений, рассматривая набор значений Ri как статистический набор данных. Пренебрегая инструментальной погрешностью, получим:

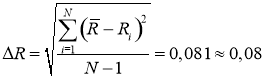(Ом).

Итак,Ом.

Это самый простой, но не лучший способ выбора коэффициента k в случае, когда сглаживающая зависимость между величинами xи y линейная и имеет вид: y = kx.

Способ № 2 (Метод наименьших квадратов)

1.                Значение сопротивления R можно найти по формуле:

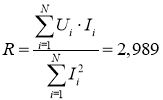(Ом).

2.                Погрешность вычислим по формуле:

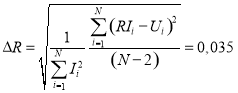(Ом).

В результате получим: (Ом).

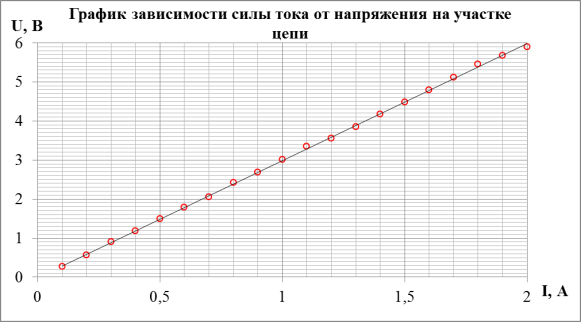
Видно, что наиболее вероятные значения сопротивлений, вычисленные двумя рассмотренными способами, попадают в доверительные интервалы друг друга и, следовательно, оба имеют право на существование. Однако погрешность расчета сопротивления при использовании метода наименьших квадратов оказалась вдвое меньше по сравнению с первым способом. Таким образом, результат, полученный методом наименьших квадратов, более точен.

Литература:

1.                Тейлор Дж. Введение в теорию ошибок / Дж. Тейлор; Пер. с англ. М.: Мир, 1985. 272 с.
2.                Исаков В. А. Физика колебаний. Лабораторный практикум: Методические указания к лабораторным работам по физике / В. А. Исаков, В. П. Нестеров / Омский гос. ун-т путей сообщения. Омск, 2001. 22 с.
3.                Линник Ю. В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений / Ю. В. Линник. Л.: Физматгиз, 1962. 352 с.